Жизнь на полной мощности

своей рукой в он вырезает часть диапазона на который давит, с такой розыгрыш был бы ... правильнее что ли?

есаул, KJss труднее на терне решение принять. KJdd на терне проcто, так как эквити отличное + ФЭ + имплайды.

del

Последнее время достаточно много времени уделяю игре. При этом, стал замечать, ухудшение состояния: апатия, слабость, нежелание что-либо делать, в какой-то степени потеря себя. Не знаю, связано ли это с самой игрой, плохими результатами, или стечением обстоятельств. В любом случае я потихоньку выпал из жизни, что не очень здорово. Думаю, минимум на месяц полностью откажусь от покера и займусь развитием текущих материй. 3 месяца до нового года. Нужно хоть как-то оправдать свое существование и сделать что-нибудь полезное, а не только кнопки тыкать :)

Еще заметил, что в периоды активной игры сразу портится режим, появляется бессонница. Так повелось, что режим довольно дисперсионный. Если и удается восстановить его, то скоро он съезжает, и снова все по новой. Несмотря на любовь к игре и регварам, не хочу ощущать негативное влияние на жизнь в целом. Не стоит покер этого.

В любом случае возникает дилемма. С одной стороны я хочу играть относительно высоко, 200+. Но для качественной игры здесь нужно имхо тратить много времени на разбор раздач, отслеживание тенденций и прочее. Несмотря на свой ранг любителя, играть хочется в А-игру. Получается в любом случае нужно тратить много времени. Банально для сглаживания дисперсии нужно откатывать адекватное кол-во раздач, а не 10к в месяц.

з200 пока приостановил, дороговато, а вот з100 продолжал.

Примерно так это выглядит: 4bb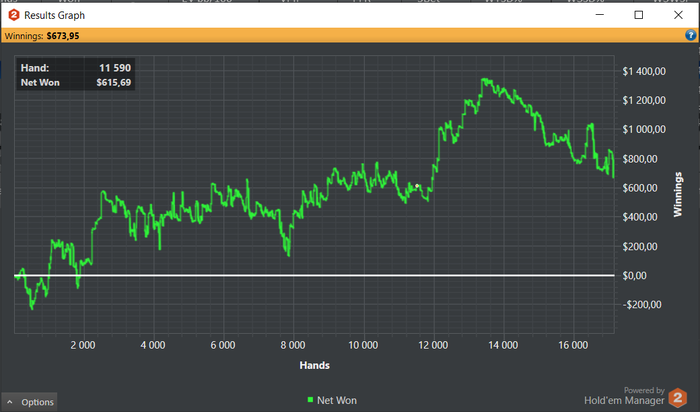


Думал сначала описать свое видение з100, з200. Но мне лень[hi, apathy], да и нечего говорить особо.
В общем я ухожу, не знаю насколько, минимум на месяц, а может и навсегда, как пойдет. Не готов жертвовать качеством жизни ради покера.

Всем гл.

Несмотря на паузу в покере, из блога никуда уходить не собираюсь. Продолжу спамить)

Хочется поделиться некоторыми видео, которые я пересматриваю чуть ли не ежедневно.

Одно из лучших исполнений Ван Халена. Леденящий душу момент с 5:00.


Клавишный кавер на одну из песен Warmen(сольный проект Янне Вирмана - клавишник финской метал группы Children of Bodom).


Кавер на соло из песни группы Dark Tranquilty - Lost to apathy. Эпик с 0:34.


И еще два:

А как ты в 21 год уже в маге вмк учился? Гений что-ли?

arsenalua, Ахах. Да просто в школу в 6 лет пошел. В универ соответственно в 17 лет, 4 года бакалавриата и вот мага - 21 год.

Прошло полмесяца без техаса, абсолютно не тянет. Зато потратил последние дней 10 на прохождение ведьмака 3.

Я не особо люблю играть в компьютерные игры. Все ограничивалось каткой в кс после школы(в свое время). Другие сетевухи, такие как: dota, wow, pw, l2 не зашли абсолютно. У меня довольно мощный ноут(ACER PREDATOR HELIOS 300) с неплохой видеокартой(gtx 1080 ti). На протяжении двух лет собирался протестировать видеокарту на какой-нибудь ресурсной игре. Никак не находил мотивации для этого. Но недавно настал этот момент, и я решился протестировать на 3-м ведьмаке. Отзывы об игре хорошие, да и игра вроде относительно требовательная к железу. После первых часов игры, сложилось ощущение, что это одна из лучших игр из всех существующих(хоть я и не игрок, периодически смотрю летсплеи на ютубе или курю новости индустрии). Не буду говорить, что она идеальная на 100%, но графика отменная(если на максималках играть), квесты интересные, мир разнообразен, персонажи и чудовища со своей историей, интересный и драматичный сюжет, диалоги, взаимодействия персонажей между собой. Имхо это все на очень высоком уровне. В процессе игры все доходило до того, что просто не можешь идти спать, так как интересно, что будет дальше, как развернутся события. Процесс похож на просмотр топового сериала или на чтение изумительной книги.



В один из дней я провел за игрой ровно сутки с минимальными перерывами(личный рекорд).
Основной сюжет(не берем в рассмотрение дополнения игры) имеет разные концовки. Можно получить несколько вариантов. Моя концовка оказалась самой грустной. Настолько опустошенным я давно себя не чувствовал, чуть было не пустил слезу от произошедшего.

Погрустив пару дней, продолжил играть в дополнения(Каменные сердца, Кровь и вино). Каменные сердца уже пройдены. Осталось пройти Кровь и Вино. Здесь тоже события разворачиваются довольно интересным образом.

Нужно успеть пройти до вечера воскресенья, ведь в понедельник выхожу на новое место работы)

Конец истории. Ведьмак 3 полностью пройден. Это были потрясающие 2 недели.

Начинается новая игра. Игра в жизнь...

Обожаю математику. Провел полные 2 дня в поту над рядом задач.

В связи с этим вот вам 2 простенькие задачи.

1. Лыжник проехал один круг со скоростью 10км/ч. С какой скоростью он должен проехать 2-й круг, чтобы средняя скорость за все 2 круга составила 20км/ч ?

2. Игра с кубиком. Бросаем кубик 1-й раз и у нас есть опции: забрать столько рублей, сколько выпало на кубике или бросить еще раз и тогда забрать столько рублей, сколько выпало во 2-й раз. Какой стратегии придерживаться, чтобы был наилучший денежный профит? (могут выпасть числа на кубике 1,2,3,4,5,6). Какое денежное ожидание в выбранной стратегии?

Вот ещё интересная, сложная задача:
Имеется 12 монет, одна из них фальшивая, но мы не знаем, она легче или тяжелее.
Есть рычажные весы. Как определить фальшивую монету за 3 взвешивания?

Algotrader @ 27.10.2019
Обожаю математику.

Если бы все любители, как ты себя называешь, были похожи на тебя, то в покере было бы сложнее наживать, особенно гуманитариям.

1. 30км в час? просто посчитал среднее арифметическое, но я думаю что там, наверное, какой-то подвох.
2. стратегия: если выпало 1,2,3 кидать еще раз, если выпало 4,5,6 забирать кэш. Как ожидание посчитать не знаю.

daniska,
Большое спасибо за задачу. Часа полтора пропотел.

Решение под катом.

toa,

1. Подвох офк. Попробуй сам подумать еще. Подсказка: какая формула средней скорости по определению?
2. Стратегия верная(интуитивно понятно), но неплохо бы доказать, хех.
Под кат вынесу краткий расчет мат.ожидания:

Algotrader, красааава!

2. интуитивно не слоажная, верно. У нас 50\50 что выпадет 1,2,3 или 4,5,6. Если в первый раз выпало число из младшей группы, то имеет смысл перекинуть и попробовать получить число из старшей группы т.к. у нас есть 50% что выпадет 4,5,6. Если же сразу выпало число из старшей группы, 4 или 5, то нет смысла перекидывать, и пытаться получить 6, т.к. выше вероятность что выпадет меньшее число, чем максимальное. Или нужно прям формулу написать?

По 1. подумаю еще раз. как найду формулу, я прошел мимо точных наук в прошлом )

toa, Можно понять это следующим образом. Ты когда бросаешь кубик, в среднем будет 3.5. Когда ты получил 4 при первом броске. То стоит задуматься, что если ты бросишь второй раз, то в среднем будет также 3.5, что меньше 4 => не имеет смысла перебрасывать, если ты не лудоман конечно:)

1. мгновенно.

Algotrader, думаю, что при выпадение 1,2,3 надо перебрасывать. 1 и 2 это понятно, без объяснений. Но цифра 3 у нас в расход. 4 5 6 победа, а 1 и 2 проигрыш, получается три цифры на победу две на проигрыш

с лыжником получилось 13,3(3) км/ч

upd. можете начинать обоссывать