Критерий Келли
Статистика
Статистика темы
-
ПопулярностьТоп-4840
-
Постов28
-
Просмотров5,908
-
Подписок0
-
Карма автора+115
Лучшие посты автора
Лучшие посты читателей
-
Что же касается самих рисков, то сейчас у экономистов в моде VaR (Value at Risk), квантилии распреде
+1
-
Вместо среднего лучше брать медиану
+1
-
Не лучшая ссылка на критерий Келли. Лень читать оригинал, но вот выделенное утверждение, пример 2.1.
+1
-
Алгоритм -генерю число от 0 до 1, если меньше или = (1-0,53) из банка минусую часть, если больше - п
+1
-
Еще прогон Минусовых игроков 1783 из 10000 Минусовых игроков в %=17,83 Средний баланс = 35,512811885
0
-
Сообщение отредактировал helperroullet - 18.10.2012, 13:54
-
Я тут поковырялся, чтобы советов вредных не давать. Хотя и забежал вперед. Но теперь я понимаю, что делать.
Мы будем считать не конечный выигрыш, который может быть от -1, а конечный банк. Он будет от нуля.
Т.е. у кого банк меньше 1 остался, те в минусе.
Шаг возьмем 0,02. Т.е. считаем какой процент игроков попали в интервал [0;0,02) (это больше или равно 0 и меньше 0,02).
Если есть такие игроки, то получаем точку со значением (0+0,02)/2=0,01 и соответствующим процентом.
Потом [0,02;0,04). И так до конца. Потом загоняем эти точки в Эксель и строим точечный график. Получится примерно это.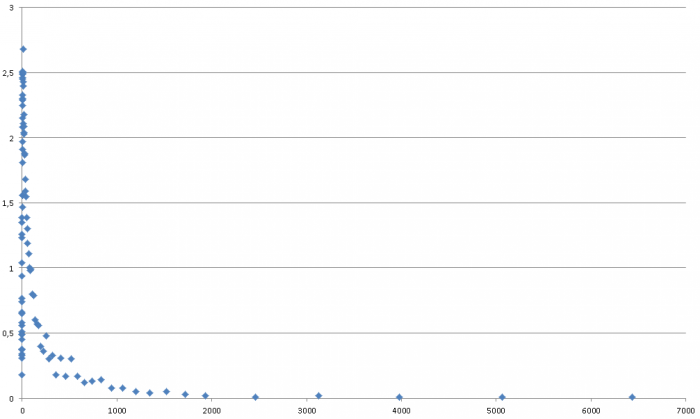
Херня полная, как видишь.
Меняем шкалу на логарифмическую.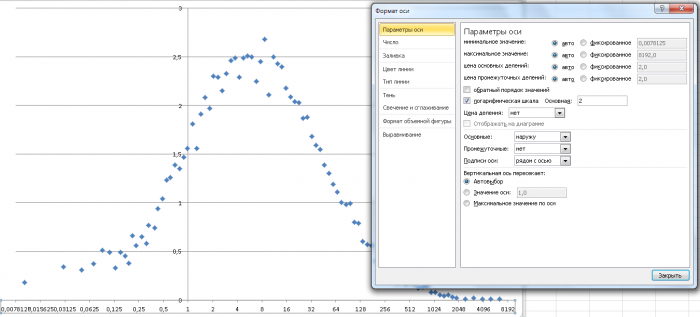
Намного лучше стало.
А чтобы вообще красиво было, я взял не 10 тыс. игроков, а 10 млн.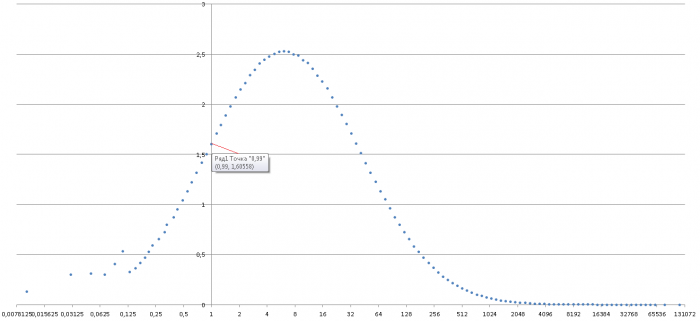
Выделенная точка означает, в частности, что с вероятностью 1,61% мы останемся примерно в нуле.
А вот данные0,01 0,13096
0,03 0,29773
0,05 0,3108
0,07 0,30197
0,09 0,40555
0,11 0,53272
0,13 0,32731
0,15 0,36572
0,17 0,41729
0,19 0,47088
0,21 0,52543
0,23 0,59083
0,27 0,65291
0,31 0,72206
0,33 0,79661
0,39 0,86997
0,43 0,95187
0,49 1,03922
0,55 1,13414
0,61 1,22253
0,69 1,31544
0,79 1,4175
0,89 1,50321
0,99 1,60558
1,13 1,70834
1,27 1,79531
1,43 1,89023
1,61 1,97997
1,83 2,06689
2,05 2,14983
2,31 2,2142
2,61 2,28943
2,95 2,34463
3,33 2,40773
3,75 2,44339
4,23 2,47679
4,77 2,50133
5,37 2,52421
6,05 2,5306
6,83 2,52335
7,71 2,49906
8,69 2,48942
9,79 2,44169
11,05 2,41132
12,45 2,3564
14,05 2,28875
15,83 2,22784
17,85 2,15841
20,13 2,06978
22,71 1,98031
25,61 1,89385
28,87 1,80351
32,57 1,70719
36,71 1,60598
41,41 1,51356
46,69 1,41321
52,65 1,31734
59,37 1,22571
66,95 1,13415
75,49 1,05406
85,13 0,96424
96,01 0,87337
108,27 0,80023
122,09 0,72181
137,67 0,65247
155,25 0,58295
175,05 0,52961
197,41 0,47084
222,61 0,41703
251,03 0,36616
283,07 0,32274
319,21 0,28072
359,95 0,24509
405,91 0,21382
457,73 0,18637
516,17 0,16144
582,05 0,1413
656,37 0,11754
740,15 0,09979
834,63 0,08538
941,19 0,07187
1061,33 0,06251
1196,83 0,05155
1349,61 0,04152
1521,91 0,03511
1716,19 0,0294
1935,29 0,02479
2182,33 0,0198
2460,93 0,01702
2775,09 0,01362
3129,37 0,01055
3528,85 0,00883
3979,35 0,0072
4487,35 0,00568
5060,21 0,00439
5706,19 0,0038
6434,65 0,00305
7256,09 0,00245
8182,39 0,00159
9226,95 0,00149
10404,87 0,00097
11733,15 0,00084
13230,99 0,0008
14920,05 0,00049
16824,75 0,00043
18972,59 0,00035
21394,61 0,00028
24125,85 0,00018
27205,75 0,00019
30678,81 0,0001
34595,27 9,00E-05
39011,67 5,00E-05
43991,89 1,00E-05
49607,87 3,00E-05
55940,79 2,00E-05
63082,17 1,00E-05
80216,31 3,00E-05
115026,19 1,00E-05
Для Хелпера
У меня прогон для 10млн игроков занял около получаса. На сортировку результатов и расчет таблицы - секунды 3. Ну а потом в текстовый csv и в Эксель.
Но я использовал "быструю сортировку". Пузырек повешается на 10 млн. Лучше, имхо, тогда вообще без сортировки.
Для интереса возьмем шаг не 0,02, а 1. Первая точка 0,5 соответствует интервалу [0;1) - вероятность остаться в минусе.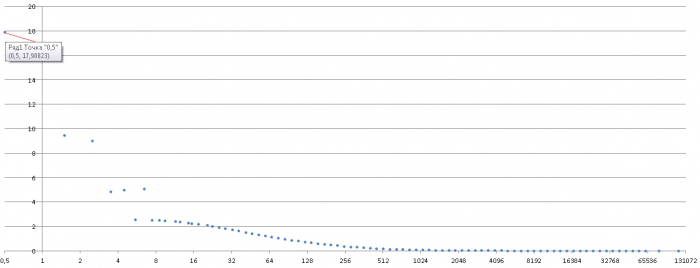
Сообщение отредактировал Contriver - 18.10.2012, 15:12 -
Хелпер! Такой вопрос, пока графики делаешь.
Ты - владелец сети фастлудов. Их всего у тебя 10к по миру. Каждому фастлуду ты дал по 1 у.е. оборотки.
После того, как они отыграют по 1000 раундов, они принесут всю выручку тебе.
И тебя менеджеры спрашивают: "А по какой ставочной стратегии играть каждому фастлуду?"
Сколько нам ставить от банка: 4%, 6 или 8? (я для простоты беру заданные варианты).
Какой-то прыщавый выпускник тебе робко заикается, что ставить нужно 6%, т.к. он где-то вычитал, что это по Келли, типа круто, "оптимальный рост капитала" и все такое.
Что ты выберешь? Твоя задача урожай больше собрать. -
Вместо среднего лучше брать медиану
-
Спасибо. Посчитаем, сравним. Я и не знал про нее. Хотя когда-то может и знал. Слово знакомое. Не только из геометрии. Вот квантиль даже вспомнить не могу.
Итак, что я вычитал про медиану из Вики.
Медиа́на (50-й процентиль, квантиль 0,5) — возможное значение признака, которое делит ранжированную совокупность (вариационный ряд выборки) на две равные части: 50 % «нижних» единиц ряда данных будут иметь значение признака не больше, чем медиана, а «верхние» 50 % — значения признака не меньше, чем медиана.
Медиана является важной характеристикой распределения случайной величины и так же, как математическое ожидание, может быть использовано для центрирования распределения. Однако, медиана более робастна и поэтому может быть более предпочтительной для распределений с т.н. тяжёлыми хвостами.
Медиана определяется для широкого класса распределений (например, для всех непрерывных), а в случае неопределённости, естественным образом доопределяется (см. ниже), в то время как математическое ожидание может быть не определено (например, у распределения Коши).
Пример использования
Предположим, что в одной комнате оказалось 19 бедняков и один миллиардер. Каждый кладет на стол деньги — бедняки из кармана, а миллиардер из чемодана. По пять долларов кладет каждый бедняк, а миллиардер — $1 млрд (109). В сумме получается $1 000 000 095. Если мы разделим деньги равными долями на 20 человек, то получим $50 000 004,75. Это будет среднее арифметическое значение суммы наличных, которая была у всех 20 человек в этой комнате.
Медиана в этом случае будет равна $5 (полусумма десятого и одиннадцатого, срединных значений ранжированного ряда). Можно интерпретировать это следующим образом. Разделив нашу компанию на две равные группы по 10 человек, мы можем утверждать, что в первой группе каждый положил на стол не больше $5, во второй же не меньше $5. В общем случае можно сказать, что медиана это то, сколько принес с собой средний человек. Наоборот, среднее арифметическое — неподходящая характеристика, так как оно значительно превышает сумму наличных, имеющуюся у среднего человека.
Неуникальность значения
Если имеется чётное количество случаев и два средних значения различаются, то медианой, по определению, может служить любое число между ними (например, в выборке {1, 2, 3, 4} медианой, по определению, может служить любое число из интервала (2,3)). На практике в этом случае чаще всего используют среднее арифметическое двух средних значений.
Т.о. мы должны отсортировать наш массив конечных банков. Для случая с 10к игроками медианой будет любое число между 5000-м и 5001-м элементом в отсортированном массиве. Возьмем среднее.
В Экселе можно тоже посчитать. Там не обязательно сортировать. -
-
Сделал 5 графиков с 4%, 5%, 6%, 7%, 8% от ставки. 10 млн. игроков. Остальные условия прежние.
Шаг сделал динамическим, чтобы не было выбиваний в графиках.
На N-м шаге диапазон увеличивается на (1,025^N)/10000. На глазок формулу взял.
Теперь у нас шажочки очень маленькие в начале и огромные скачки в конце.
И вот что получилось.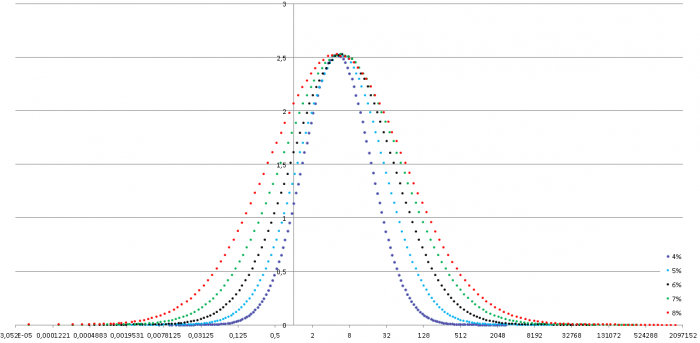
С ростом ставки крылья расправляются.
Но тут важно помнить, что шкала логарифмическая. Правое крыло очень длинное.
Келли наш посередине. Чем же он так примечателен?
Для ответа мы составим таблицу.
Хелпер, сделаешь таблицу? Если времени нет, я могу.
Типа такой
--------------- Медиана | % в минусе | МО | Максим. конечный банк
%%
2
4
5,5
6
6,5
8
10
Можно СКО еще посчитать конечных банков.
Сообщение отредактировал Contriver - 19.10.2012, 12:10 -
Что же касается самих рисков, то сейчас у экономистов в моде VaR (Value at Risk), квантилии
распределения. Это сегодняшний день. Дисперсия, в качестве меры риска это вчерашний день.
В математику уже входит CVaR(Conditional Value at Risk). Условное матаматическое ожидание,
при том, что случайная величина меньше наперед заданного значения. Это завтрашний день.
Использовать их в гэмблинге? Что это даст? Лучше оценим происходящие в игре процессы? Но
позволит ли это больше выигрывать? Все, что нужно для успешной игры, мне кажется, вам
известно. Извечная проблема банк и время. Но это проблема для всех, у кого сколько бы не
было. Прибыль будет соразмерна с нашим капиталом. Что тут удивительного.
Размер ставки и риски. Про Келли всем известно. В этой области исследования продолжаются.
(Правда мало кто представляет себе, что это стратегия фактически стратегия-мартингал. Не
ставки по мартингалу, а банк по мартингалу). Сегодня в авангарде этих исследований стоит Сид
Браун (Sid Browne). В интернете у него страничка. -
http://www2.gsb.columbia.edu/divisions/dro/browne_research.html -
Поскольку у нас повелось на графиках рассматривать конечные банки, а не чистые выигрыши, то и будем работать с конечными банками.
Для таблицы не стесняясь возьмем 100 млн. игроков. По 1000 игр каждый. Начальный банк, напомню, равен 1. Результаты ниже.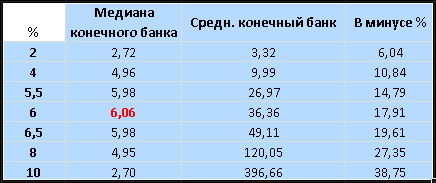
Вообще, для построения графика не нужно было искусственно создавать диапазоны и высчитывать процент попадания.
Случайные величины сами ложатся в определенные точки. Но в силу естественных потерь точности на ЭВМ я округлял до 5-го знака после запятой, а потом группировал.
Можно было и больше знаков взять. Так, например, для 6% все 100 млн. конечных результата уложились в 177 значения (все эти значения в конце поста).
Для остальных и того меньше.
Я намеренно брал такую большую дистанцию, чтобы четче увидеть, соответствует ли значение медианы вершине на графике.
Да, так и есть. За исключением 10%. Там рядом легло. Случайность это или нет - я не знаю. Разница везде очень невелика.
Ниже приведены "околомедианные" области.
2%2,05460308939171 ; 2,290461
2,13846443997913 ; 2,355608
2,22574870283541 ; 2,402669
2,31659558866543 ; 2,445101
2,41115051065178 ; 2,485359
2,50956481720899 ; 2,507658
2,61199603423793 ; 2,52213
2,71860811726805 ; 2,52667
2,82957171389124 ; 2,521937
2,9450644369072 ; 2,506868
3,0652711486177 ; 2,481042
3,19038425672454 ; 2,448881
3,32060402230514 ; 2,405437
3,45613888035841 ; 2,352987
3,59720577343427 ; 2,291225
4%2,83018362017512 ; 2,289566
3,06603225518972 ; 2,350503
3,32153494312219 ; 2,400307
3,59832952171571 ; 2,448998
3,89819031519202 ; 2,479439
4,22303950812469 ; 2,506877
4,57495946713508 ; 2,521009
4,95620608939634 ; 2,528958
5,3692232635127 ; 2,521552
5,81665853547209 ; 2,506364
6,30138008009476 ; 2,480267
6,82649508676932 ; 2,44789
7,39536967733344 ; 2,40456
8,01165048377789 ; 2,352805
8,67928802409271 ; 2,29451
5,5%2,76699928774861 ; 2,289166
3,0890838609257 ; 2,350501
3,44865976008107 ; 2,403501
3,85009105490532 ; 2,446796
4,29824980203716 ; 2,480826
4,79857517581926 ; 2,507538
5,35713948199928 ; 2,519735
5,98072185556533 ; 2,527492
6,67689053716553 ; 2,523739
7,45409472667686 ; 2,508588
8,3217671287239 ; 2,483879
9,29043843471293 ; 2,446155
10,3718651308171 ; 2,408678
11,5791721830815 ; 2,349734
12,9270123313767 ; 2,293275
6%2,61188289072543 ; 2,288929
2,94531474911591 ; 2,348792
3,32131237666262 ; 2,40146
3,74530970134295 ; 2,446157
4,22343434406759 ; 2,478248
4,76259617522515 ; 2,507104
5,37058717631772 ; 2,522371
6,0561940498902 ; 2,526169
6,82932520519533 ; 2,521969
7,70115395479473 ; 2,505185
8,68427999157704 ; 2,482053
9,79291147986347 ; 2,449538
11,0430703921865 ; 2,405135
12,4528240592741 ; 2,351143
14,042546279607 ; 2,292711
6,5%2,40427008283225 ; 2,2879
2,73855362376079 ; 2,348629
3,11931509016604 ; 2,402485
3,55301665350463 ; 2,445736
4,04701896896517 ; 2,479894
4,60970609834 ; 2,506588
5,25062780185252 ; 2,523325
5,98066161387479 ; 2,53103
6,81219745323707 ; 2,521413
7,75934790128072 ; 2,508622
8,83818771643205 ; 2,481773
10,0670266502675 ; 2,448479
11,4667201952245 ; 2,406073
13,061023537876 ; 2,353159
14,8769947249604 ; 2,291129
8%1,61219571864799 ; 2,289196
1,89257758276068 ; 2,351327
2,22172151019732 ; 2,398922
2,60810785979686 ; 2,446672
3,06169183541371 ; 2,484799
3,59415998070304 ; 2,508846
4,21923128169488 ; 2,520294
4,95301063503312 ; 2,528084
5,81440378895192 ; 2,520896
6,82560444790008 ; 2,507915
8,01266609101313 ; 2,483276
9,40617323727629 ; 2,448796
11,0420294524548 ; 2,404784
12,9623824007078 ; 2,352663
15,2167097747439 ; 2,291171
10% Здесь медиана не на вершине!0,663821539713557 ; 2,289443
0,81133743742768 ; 2,349004
0,991634645744942 ; 2,401341
1,21199790035493 ; 2,444459
1,48133076710047 ; 2,482102
1,81051538201169 ; 2,506797
2,21285213356984 ; 2,525271
2,70459705214091 ; 2,52235
3,30561861928334 ; 2,520911
4,04020053467964 ; 2,50637
4,93802287571955 ; 2,482806
6,03536129254612 ; 2,450636
7,3765526908897 ; 2,407736
9,01578662219853 ; 2,35195
11,0192947604649 ; 2,292499
Все уникальные значения для 6%0,000155072488303066 ; 2E-6
0,000174868976171542 ; 2E-6
0,000197192675257271 ; 1E-6
0,000222366208268838 ; 3E-6
0,000282764454063904 ; 3E-6
0,000318862043944403 ; 4E-6
0,00035956783678837 ; 2E-6
0,000405470113825181 ; 4E-6
0,00045723225601563 ; 9E-6
0,000515602331251668 ; 1,2E-5
0,000581423905454009 ; 1,2E-5
0,00065564823380984 ; 2,3E-5
0,000739348008338755 ; 3,3E-5
0,000833732860467107 ; 4E-5
0,000940166842654396 ; 6,1E-5
0,00106018814171666 ; 7,8E-5
0,00119553130874432 ; 8,9E-5
0,00134815232688189 ; 0,000128
0,00152025687924979 ; 0,000195
0,001714332225537 ; 0,000214
0,00193318314794597 ; 0,000339
0,00217997248598163 ; 0,000416
0,00245826684589418 ; 0,000529
0,00277208814537003 ; 0,000711
0,003125971738396 ; 0,000893
0,00352503196031889 ; 0,001169
0,0039750360403596 ; 0,001488
0,0044824874497672 ; 0,001869
0,00505471989016302 ; 0,002435
0,00570000328039659 ; 0,002971
0,00642766327363871 ; 0,003726
0,00724821603197556 ; 0,004701
0,00817352020627032 ; 0,005981
0,00921694831770907 ; 0,007503
0,0103935800178422 ; 0,009019
0,0117204200201199 ; 0,01126
0,0132166438524756 ; 0,013816
0,0149038749825789 ; 0,016918
0,0168064973207804 ; 0,020658
0,0189520076170503 ; 0,025111
0,0213714128447588 ; 0,03023
0,0240996783143025 ; 0,03648
0,0271762329927241 ; 0,04372
0,0306455393322208 ; 0,051654
0,034557735842717 ; 0,062164
0,0389693616949788 ; 0,07396
0,0439441738262527 ; 0,087182
0,0495540683572637 ; 0,102474
0,0558801196369143 ; 0,119767
0,0630137519309885 ; 0,138969
0,0710580606881359 ; 0,162437
0,0801293024781108 ; 0,187782
0,0903585751348908 ; 0,216375
0,101893712386153 ; 0,248942
0,114901420350343 ; 0,284748
0,129569686778047 ; 0,324241
0,146110497856095 ; 0,36823
0,164762901837724 ; 0,414808
0,185796463774455 ; 0,467818
0,209515161277577 ; 0,524937
0,236261777610885 ; 0,58573
0,266422855603764 ; 0,651829
0,300434283978712 ; 0,720662
0,338787596827058 ; 0,793652
0,382037077273066 ; 0,8721
0,430807767988776 ; 0,957353
0,485804504327769 ; 1,041644
0,547822100624931 ; 1,131889
0,617756836874923 ; 1,222686
0,696619411795125 ; 1,318542
0,785549549471099 ; 1,416338
0,885832470680175 ; 1,507755
0,998917466937218 ; 1,607488
1,12643884569516 ; 1,702544
1,27023954940093 ; 1,79792
1,43239778974998 ; 1,891734
1,61525708205849 ; 1,983181
1,82146011381064 ; 2,066977
2,05398693685029 ; 2,146441
2,31619803517161 ; 2,222311
2,61188289072543 ; 2,288929
2,94531474911591 ; 2,348792
3,32131237666262 ; 2,40146
3,74530970134295 ; 2,446157
4,22343434406759 ; 2,478248
4,76259617522515 ; 2,507104
5,37058717631772 ; 2,522371
6,0561940498902 ; 2,526169
6,82932520519533 ; 2,521969
7,70115395479473 ; 2,505185
8,68427999157704 ; 2,482053
9,79291147986347 ; 2,449538
11,0430703921865 ; 2,405135
12,4528240592741 ; 2,351143
14,042546279607 ; 2,292711
15,83521176211 ; 2,224627
17,856728157273 ; 2,149371
20,1363104752227 ; 2,071784
22,7069033018469 ; 1,986639
25,6056569148486 ; 1,894295
28,874464180574 ; 1,806078
32,56056599086 ; 1,70741
36,7172339896932 ; 1,613135
41,4045404564625 ; 1,515035
46,6902264721812 ; 1,415856
52,6506809154383 ; 1,318855
59,3720444365581 ; 1,226515
66,9514543646293 ; 1,135729
75,4984485388374 ; 1,044331
85,136548352306 ; 0,958225
96,0050438866429 ; 0,875365
108,261006936001 ; 0,795413
122,081561012938 ; 0,72165
137,666441142249 ; 0,650052
155,240880437004 ; 0,584918
175,058865173643 ; 0,525264
197,406805408576 ; 0,46724
222,607674184139 ; 0,415357
251,025675143816 ; 0,367805
283,07150601324 ; 0,32315
319,20829401493 ; 0,283473
359,95828899556 ; 0,248591
405,910410994993 ; 0,216121
457,728761334779 ; 0,186283
516,162220228581 ; 0,161447
582,055269619464 ; 0,138207
656,36019765599 ; 0,118867
740,150861186543 ; 0,101238
834,638205167804 ; 0,085864
941,187763274332 ; 0,072355
1061,3393926285 ; 0,06124
1196,82952785767 ; 0,051372
1349,61627609482 ; 0,043035
1521,90771559629 ; 0,035724
1716,19380694901 ; 0,029344
1935,28237804888 ; 0,024239
2182,33970290619 ; 0,020116
2460,936260724 ; 0,016562
2775,0983365611 ; 0,013413
3129,36620931358 ; 0,010919
3528,85976794936 ; 0,008814
3979,35250428332 ; 0,007014
4487,35495163864 ; 0,005516
5060,20877525208 ; 0,004593
5706,19287422044 ; 0,003635
6434,64302837624 ; 0,002875
7256,08681923278 ; 0,002181
8182,39577487951 ; 0,001828
9226,95693763009 ; 0,001356
10404,8663339233 ; 0,001055
11733,1471425092 ; 0,00082
13230,9957138934 ; 0,00066
14920,0589965181 ; 0,000525
16824,7473790523 ; 0,000379
18972,5874699952 ; 0,00026
21394,6199129733 ; 0,000241
24125,8479869699 ; 0,000139
27205,7434746682 ; 0,000129
30678,8171097322 ; 9,7E-5
34595,2618471449 ; 6,2E-5
39011,6782531633 ; 6E-5
43991,892498248 ; 4,4E-5
49607,87877462 ; 4,1E-5
55940,7994692525 ; 2,2E-5
63082,1781249018 ; 1,4E-5
71135,2221408467 ; 1,3E-5
80216,3143290399 ; 6E-6
90456,6948816832 ; 3E-6
102004,358058068 ; 8E-6
115026,191001652 ; 3E-6
129710,385597607 ; 4E-6
146269,158227089 ; 1E-6
164941,816724164 ; 4E-6
185998,218859164 ; 1E-6
236518,332628064 ; 1E-6
339155,483916552 ; 1E-6
ВЫВОДЫ СЛЕДУЮТ!
Сообщение отредактировал Contriver - 21.10.2012, 22:32
28 постов
Подписаться на обновления темы по почте
1 человек читает эту тему (1 гость):
Зачем регистрироваться на GipsyTeam?
- Вы сможете оставлять комментарии, оценивать посты, участвовать в дискуссиях и повышать свой уровень игры.
- Если вы предпочитаете четырехцветную колоду и хотите отключить анимацию аватаров, эти возможности будут в настройках профиля.
- Вам станут доступны закладки, бекинг и другие удобные инструменты сайта.
- На каждой странице будет видно, где появились новые посты и комментарии.
- Если вы зарегистрированы в покер-румах через GipsyTeam, вы получите статистику рейка, бонусные очки для покупок в магазине, эксклюзивные акции и расширенную поддержку.


Минусовых игроков 1783 из 10000
Минусовых игроков в %=17,83
Средний баланс = 35,5128118853859 ед.
Максимальная ставка которая была выигрышной = 505,029345811342 ед.
Максимальный банк = 8922,18510933371 ед.
Непонятно почему минус, у нас нет вообще игроков даже с 0. Я так понимаю выигрыш - это размер банка после 1000раундов который больше 1. Тогда диапазон от 1 до МАХ. Пока так и делаю.